4 The Synchrotron – A Case Study
Discussion Topics…
- phase stability
- longitudinal motion – synchrotron oscillations
- history of the discovery of strong focusing
- matrix analysis of the AG system
Homework Problem 1:
c = 2.9979e8 # m/s
F = 3 # m
L = 0.5 # m
Ns = 20
C = 8*L*Ns
Bmax = 2 # T
Tr = 0.5 # s; max ramp time
pf = 0.8
h = 2
E0 = 938 # MeV (mc^2, proton)
E1 = 100 # MeV
E2 = 1000 # MeV
phi_s = 28*pi/180Imagine a synchrotron with circumference \(C\) = 80 m, where 80 % of the circumference contains bending magnets. It will accelerate a proton beam from a kinetic energy of 100 MeV to 1000 MeV, with a uniform rate of momentum gain, using a radio-frequency (RF) cavity. The magnets can ramp no faster than 2 T in 0.5 s.
- What will be the magnetic field strengths required to keep the beam on orbit at its initial and maximum kinetic energies?
# Brho = p/e = 10/3 (pc)_GeV
R = C/2/pi
rho = R*pf
gam_1 = (E0+E1)/E0
pc_1 = sqrt(gam_1^2 - 1)*E0
Brho_1 = 10/2.9979*(pc_1/1000)
B_1 = Brho_1/(rho)
gam_2 = (E0+E2)/E0
pc_2 = sqrt(gam_2^2 - 1)*E0
Brho_2 = 10/2.9979*(pc_2/1000)
B_2 = Brho_2/(rho)
B_1; B_2 # Tesla## [1] 0.1455715## [1] 0.5553633- Approximately how long will it take to accelerate the beam between its initial and final energies?
Bdot = 2/0.5 # Tesla/sec
dt = (B_2-B_1)/Bdot
dt # seconds## [1] 0.102448- What average voltage will the RF cavity need to produce, assuming a constant synchronous phase of 28 degrees?
# B rho = p/e rho = pf * R pdodt = e rho Bdot
# W = (gamm - 1)*mc^2
# Wdot = gamdot mc^2 = beta * c * pdot = f_0 eV sin(phi_s)
# f_0 = beta * c / (2 pi R)
# ---> 2 pf * pi R^2 * Bdot = V sin(phi_s)
#
Vrf = 2*pf*pi*R^2*Bdot/sin(phi_s)
Vrf/1000 # kV## [1] 6.942898- Assuming a harmonic number of \(h\) = 2, make a plot of the RF frequency required over the above kinetic energy range of the protons.
f_rf = function(x){ h*c/(2*pi*R)*sqrt( 1 - (E0/(E0+x))^2) }
curve(f_rf(x)/1e6,E1,E2,
xlab="kinetic energy (MeV)", ylab="RF frequency (MHz)")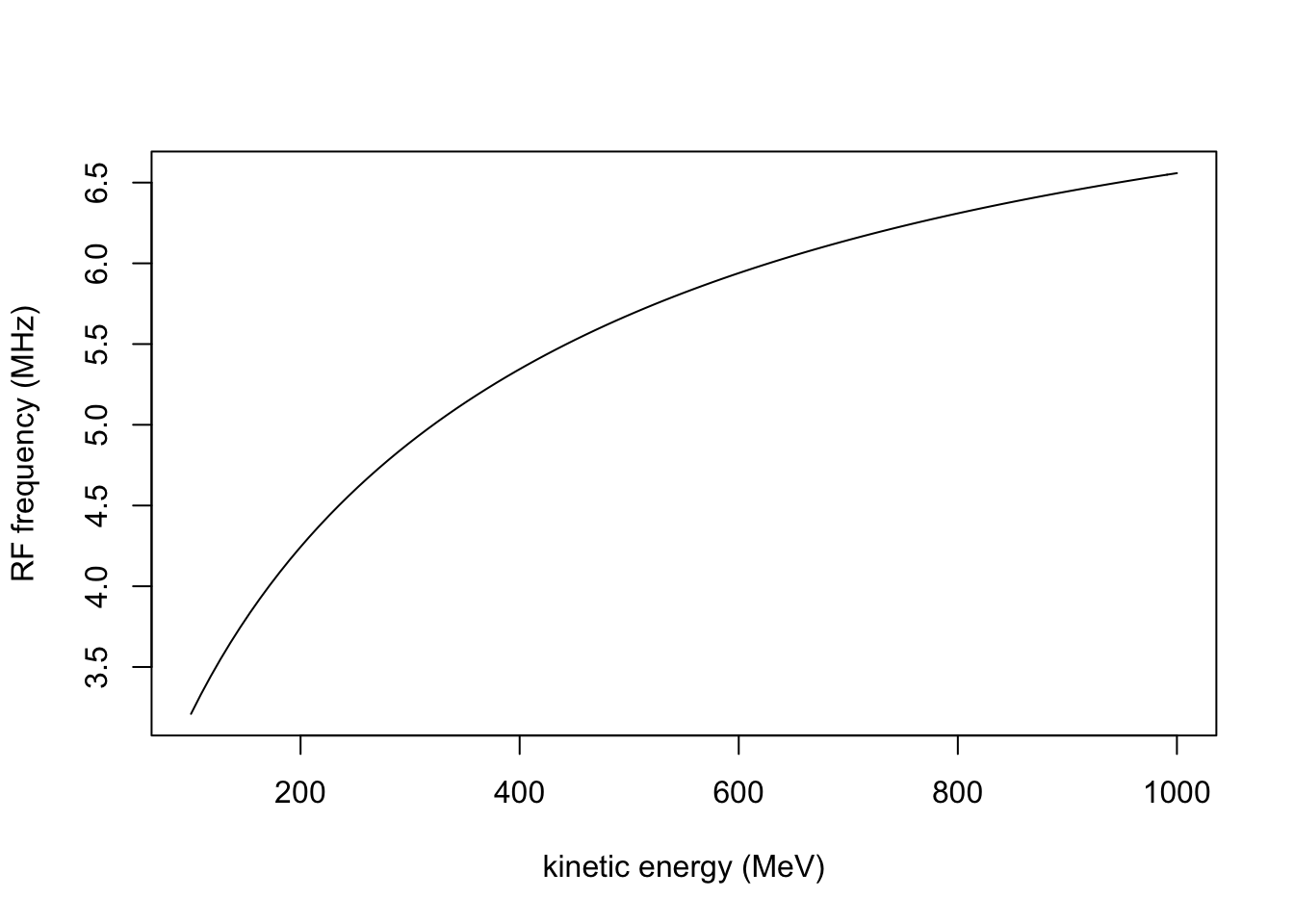
Homework Problem 2:
Consider a system made of thin lens quadrupoles with the following arrangement: FOOFODOOOODO
Here, F represents a horizontally focusing lens with focal length \(F\) = 3 m, D represents a horizontally defocusing lens of focal length \(-F\), and O represents a drift space of length \(L\) = 0.5 m.
- Determine if the system is stable in each plane \((x, y)\). If it is, determine the phase advance in degrees through the system for each plane.
Mf = matrix(c( 1, 0,
-1/F, 1), nrow=2, ncol=2, byrow=TRUE)
Md = matrix(c( 1, 0,
1/F, 1), nrow=2, ncol=2, byrow=TRUE)
Mo = matrix(c( 1, L,
0, 1), nrow=2, ncol=2, byrow=TRUE)
Mf## [,1] [,2]
## [1,] 1.0000000 0
## [2,] -0.3333333 1Md## [,1] [,2]
## [1,] 1.0000000 0
## [2,] 0.3333333 1Mo## [,1] [,2]
## [1,] 1 0.5
## [2,] 0 1.0Mx = Mo %*% Md %*% Mo %*% Mo %*% Mo %*% Mo %*% Md %*% Mo %*% Mf %*% Mo %*% Mo %*% Mf
My = Mo %*% Mf %*% Mo %*% Mo %*% Mo %*% Mo %*% Mf %*% Mo %*% Md %*% Mo %*% Mo %*% Md
Mx## [,1] [,2]
## [1,] -0.7530864 4.703704
## [2,] -0.5802469 2.296296My## [,1] [,2]
## [1,] 1.8765432 3.0740741
## [2,] -0.5061728 -0.2962963tMx = sum(diag(Mx))
tMy = sum(diag(My))
tMx## [1] 1.54321tMy## [1] 1.580247mu_x = acos(tMx/2)
mu_y = acos(tMy/2)
mu_x*180/pi; mu_y*180/pi## [1] 39.50177## [1] 37.80295- For a synchrotron made up of 20 such sections, provided that the motion is stable, determine the betatron oscillation tunes \((\nu_x, \nu_y)\) of the synchrotron for each degree of freedom.
nu_x = mu_x * Ns / 2/pi
nu_y = mu_y * Ns / 2/pi
nu_x; nu_y## [1] 2.194543## [1] 2.100164