3 The Betatron – A Case Study
Discussion Topics…
- the betatron principle
- the need for transverse focusing
- weak focusing
- transverse stability – betatron oscillations, tune space
- matrix description of the motion
- phase space
Homework Problem 1:
Consider an electron betatron with orbit radius \(R\) = 0.4 m which produces a maximum particle momentum of 42 MeV/c. Suppose the height of the magnet gap in which the beam tube resides is \(g\) = 15 cm, and that the radius of the central yoke is half the orbit radius (\(a = R/2\)) as depicted in the Figure below.
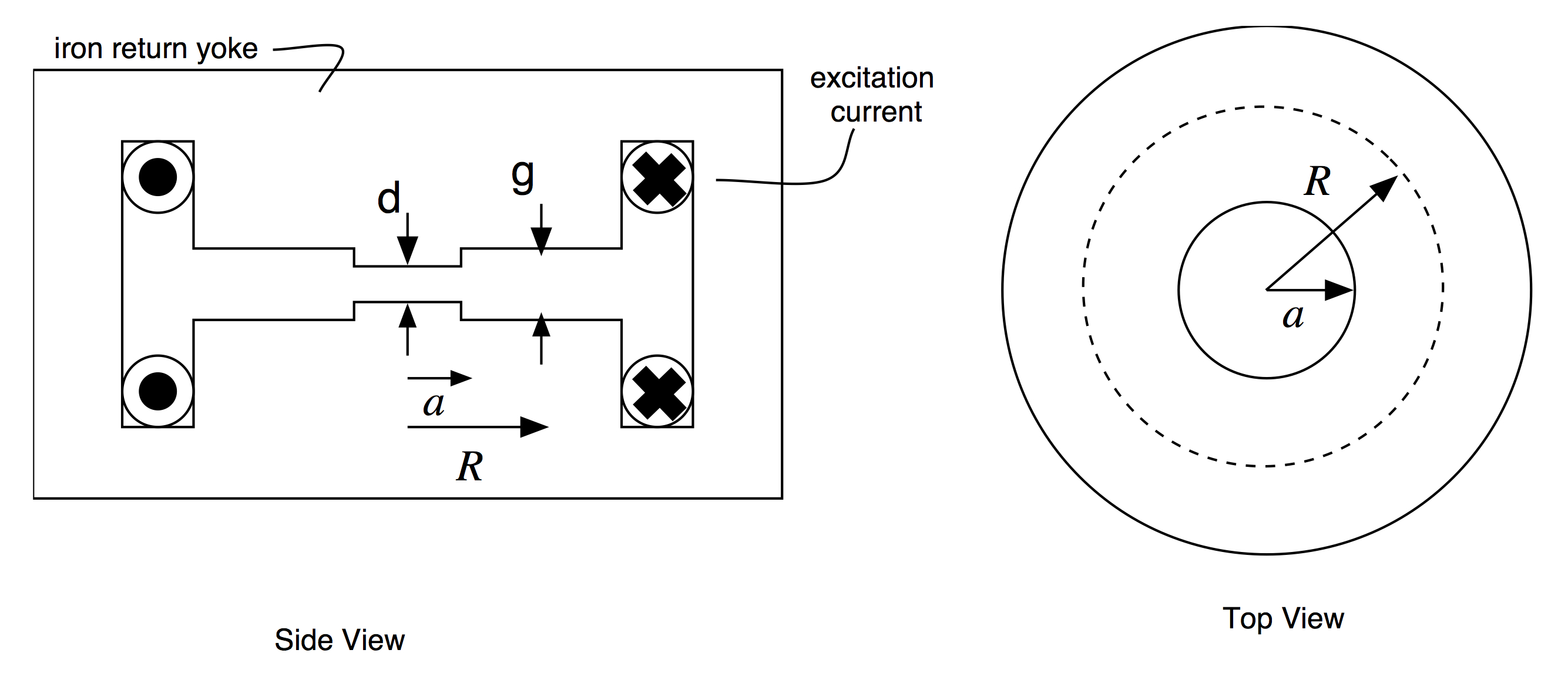
Schematic of Betatron magnet.
- For simplicity, imagine the field to be uniform with strength \(B_a\) for \(0<r<a\) and uniform with strength \(B_0\) between \(a<r<R\) (and beyond, to the outer edge of the magnet).
- What value of \(B_0\) is required at radius \(R\)?
Brho = 10/2.9979*pc/1000
B0 = Brho/R
B0 # Tesla[1] 0.3502452
- Find the height of the central yoke gap, \(d\), and the maximum total current (\(N\times I\)) required in each of the two coils of the magnet to meet the Betatron condition. Here, \(I\) is the current in the coil conductor, while \(N\) is the number of times (turns) the conductor is wrapped around the yoke.
# Betatron Condition: (pi R0^2) B0 = 1/2 Phi, Phi = integral B * dA
# Phi = pi [ a^2 Ba + (R0^2-a^2) B0 ] = pi [ a^2 (g/d) + (R0^2-a^2) ] B0
# = pi [R0^2 - (1-(g/d)) a^2 ] B0
# = pi R0^2 [1 - (1-(g/d)) (a/R0)^2 ] B0 == 2 pi R0^2 B0
# 1 - (1-(g/d)) (a/R0)^2 == 2
# [(g/d) - 1 ] (1/2)^2 = 1
# So, (g/d) = 4 + 1 = 5
d = g/5
d*100 # cm[1] 3
# Integral (B/mu) dl = (Ba/mu0) * d = N*I
mu0 = 4*pi*1e-7
Ba = B0 * g/d
Ba # Tesla[1] 1.751226
Ba/mu0*d/2 # Ampere-Turns per coil (2 coils)[1] 20903.72
- To maintain vertical stability, the poles of the magnets are tapered to create a field index of value \(n = - (\partial B/\partial r)(R_0/B_0)\) = 0.23. Qualitatively, how does this affect the value of \(d\) found above?
# The flux within the radius $R0$ would increase, and so $d$
# should be increased (open the gap further) in order to restore
# the betatron condition.- With the above value of field index, \(n\), what are the horizontal and vertical betatron tunes?
nu_x = sqrt(1-n)
nu_y = sqrt(n)
nu_x[1] 0.8774964
nu_y[1] 0.4795832
Homework Problem 2:
Consider a simple harmonic oscillator with oscillation frequency \(f = \omega / 2\pi\). Suppose this represents a particle oscillating transversely about the ideal circular orbit as observed at one location in a betatron. The revolution frequency is \(f_0 = 1/T_0\). Suppose further that during one revolution the number of oscillations around the whole circumference is \(\nu\). Then, \(f = \omega/2\pi = \nu f_0\). If we observe the transverse position and transverse speed of the particle at time \(t\) we would have \[ x(t) = a\cos\omega t \]
\[ \dot{x}(t) = -\omega a\; \sin\omega t \] if the particle started with \(x = a\) and \(\dot{x} = 0\) at \(t=0\). If we observe the particle again at the same location in the accelerator one revolution later, at time \(t+T_0\), we get \[ \begin{array}{rcrcc} x(t+T_0) &=& a\cos\omega(t+T_0) &=& \;\;\;\;\; x(t)\;\cos2\pi\nu + \frac{\dot{x}(t)}{\omega} \sin 2\pi\nu \\ \dot{x}(t+T_0 ) &=& -\omega a\sin\omega(t+T_0) &=& -\omega x(t)\;\sin2\pi\nu + \dot{x}(t) \cos 2\pi\nu . \end{array} \]
Thus, we may write our two equations of the trajectory in matrix form as \[ \left( \begin{array}{c} x \\ \dot{x} \end{array} \right)_{t+T_0} = \left( \begin{array}{cc} \cos2\pi\nu & \frac{1}{\omega}\sin2\pi\nu \\ -\omega\sin2\pi\nu & \cos2\pi\nu \end{array} \right) \left( \begin{array}{c} x \\ \dot{x} \end{array} \right)_{t} \\ = M_{2\pi\nu} \left( \begin{array}{c} x \\ \dot{x} \end{array} \right)_{t} \] where \[ M_\theta \equiv \left( \begin{array}{cc} \cos\theta & \frac{1}{\omega}\sin\theta \\ -\omega\sin\theta & \cos\theta \end{array} \right) . \]
- Verify that
- \(\det M_\theta = 1\),
- \(|{\rm Tr\;} M_\theta| < 2\),
- \(M_\theta^{-1} = M_{-\theta}\), and
- \((M_\theta)^n = M_{n\theta}\).
- In particular, show that \((M_\theta)^2 = M_{2\theta}\).
- det M = cos^2(th) + sin^2(th) = 1
- Tr(M) = 2cos(th) < 2
- M_th^{-1} = (C( th), -1/w S( th) // w S( th), C( th) ) = (C(-th), 1/w S(-th) // -w S(-th), C(-th) ) = M_{-th}
d.| e. M_th^2 = ( C2-S2, 1/w (CS+SC) // -w (CS+SC), -S2+C2 ) = ( C(2th), 1/w S(2th) // -w S(2th), C(2th) ) = M_{2th}
- Notice that the matrix \(M_\theta\) can be written in the form \(M_\theta = I \cos\theta + A \sin\theta\), where \[ I = \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right), \;\;\;\; A = \left( \begin{array}{rr} 0 & \frac{1}{\omega} \\ -\omega & 0 \end{array} \right) . \] Let \[ \vec{X} = \left( \begin{array}{c} x \\ \dot{x} \end{array} \right) , \;\;\;\; S = \left( \begin{array}{rr} 0 & 1 \\ -1 & 0 \end{array} \right) ,\] and \(\vec{X}^T\) = the " transpose of \(\vec{X}\) " = \((x \;\; \dot{x})\). Show that \[ (\vec{X}^T)SA^{-1} \vec{X} \;\;\; =\;\;\; \omega \; x^2 + \frac{1}{\omega}\; \dot{x}^2 \;\;\; = \;\;\; \omega a^2.\] Note that the final result, \(\omega a^2 = a\times (\omega a)\), is the product of the maximum displacement and the maximum transverse speed.